Differentiate 3x With Steps

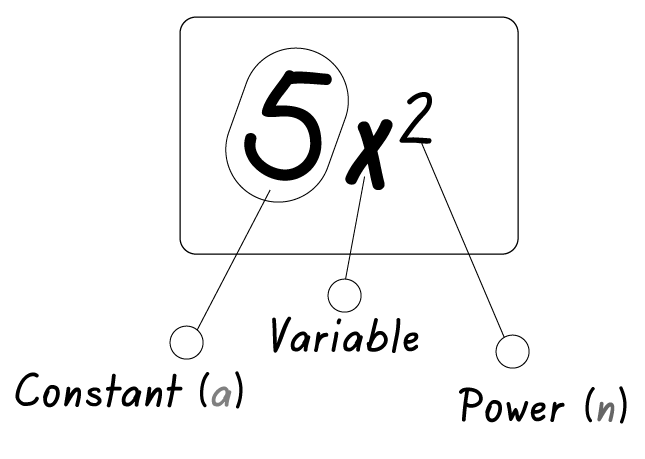
You can differentiate coefficient of x in the following form

Common functions

7

6x

x^{1/2}

2x^2

Exponential functions

-e^{-\frac{12}{7x}}

-3e^{2x}

Trigonometric functions

4 \sin (x)

-\cos(3x)

Logarithmic functions

4In9x

Learn how to differentiate the coefficient of 3x in this comprehensive guide. Brush up on your calculus skills and master the art of finding the derivative of constants in front of variables.

1. Find the derivative of the function -2x^{-\frac{1}{2}}.

Solution:

To find the derivative of a function in the form f(x) = ax^n, where a and n are constants, we use the power rule. The derivative is given by:

f'(x) = n \cdot a \cdot x^{n-1}.

Applying this rule to the given function, we have:

f'(x) = -\frac{1}{2} \cdot -2 \cdot x^{-\frac{1}{2}-1}</p><p>= x^{-\frac{3}{2}}.

Therefore, the derivative of -2x^{-\frac{1}{2}} is

x^{-\frac{3}{2}}.

2. Determine the derivative of e^{x}.

Solution:

The derivative of e^{x} is itself, as the derivative of

e^{x} is e^{x}.

This is a unique property of the exponential function e^{x}.

Therefore, the derivative of e^{x} is

e^{x}.

3. Calculate the derivative of 4\cos(9x).

Solution:
By applying the chain rule and derivative of cosine function, we have:

f'(x) = -4 \cdot 9 \sin(9x) = -36 \sin(9x).

Therefore, the derivative of 4\cos(9x) is

-36 \sin(9x).

4. Find the derivative of -3e^{\frac{8}{5}x}.

Solution:

Similarly to the derivative of e^{x}, the derivative of e^{\frac{8}{5}x} is itself times the constant \frac{8}{5}:

f'(x) = -3 \cdot \frac{8}{5} e^{\frac{8}{5}x} = -\frac{24}{5} e^{\frac{8}{5}x}.

Therefore, the derivative of -3e^{\frac{8}{5}x} is

-\frac{24}{5} e^{\frac{8}{5}x}.

5. Differentiate the function 4\sin(2x).

Solution:

Using the chain rule and derivative of the sine function, we get:

f'(x) = 4 \cdot 2 \cos(2x)= 8 \cos(2x).

Therefore, the derivative of 4\sin(2x) is

8\cos(2x).

1. \frac{d}{dx}\left(-2x^{-\frac{1}{2}}\right) = x^{-\frac{3}{2}}

2. \frac{d}{dx}\left(-e^x\right) = -e^x

3. \frac{d}{dx}\left(4\cos(9x)\right) = -36\sin(9x)

4. \frac{d}{dx}\left(-3e^{\frac{8}{5}x}\right) = -\frac{24}{5}e^{\frac{8}{5}x}

5. \frac{d}{dx}\left(5\ln x\right) = \frac{5}{x}

6. \frac{d}{dx}\left(2x^3\right) = 6x^2

7. \frac{d}{dx}\left(9e^{-2x}\right) = -18e^{-2x}

8. \frac{d}{dx}\left(7\sin(2x)\right) = 14\cos(2x)

9. \frac{d}{dx}\left(-4e^{5x}\right) = -20e^{5x}

10. \frac{d}{dx}\left(3\ln(4x)\right) = \frac{3}{x}

11. \frac{d}{dx}\left(-5\cos(3x)\right) = 15\sin(3x)

12. \frac{d}{dx}\left(6e^{-4x}\right) = -24e^{-4x}

13. \frac{d}{dx}\left(2\sin(5x)\right) = 10\cos(5x)

14. \frac{d}{dx}\left(8e^{2x}\right) = 16e^{2x}

15. \frac{d}{dx}\left(4\ln(3x)\right) = \frac{4}{x}