Getting the right result
To ensure accuracy in solving calculus problems with CalculusPop, always begin your expression with the word "differentiate." Otherwise, the AI may interpret it differently.
Click the "run CalculusPop" button to start processing your worksheet.
Provide clear and specific requests and queries to receive the most relevant results.
About Differential Calculus AI
CalculusPop differential calculus AI solver that can handle a variety of differentiation problems. It can solve equations using first principles and the general rule for differentiation of functions like y = ax^n, sine, cosine, exponential functions, and logarithmic functions.
The calculus AI also covers methods of differentiation, including the differentiation of products and quotients, functions of functions, and implicit functions. It can handle applications of differentiation such as rates of change, velocity, acceleration, turning points, maximum and minimum values, points of inflexion, tangents and normals, and small changes in functions.
The AI can also differentiate parametric equations, common parametric equations, and hyperbolic functions. Moreso, it covers logarithmic differentiation and further logarithmic functions. With its ability to solve a wide range of differentiation problems, this AI is a valuable tool for students and professionals working in calculus and related fields.
Write into the playground box as...
3x^2 \cdot \sin (2x) as 3x^2* sin (2x)
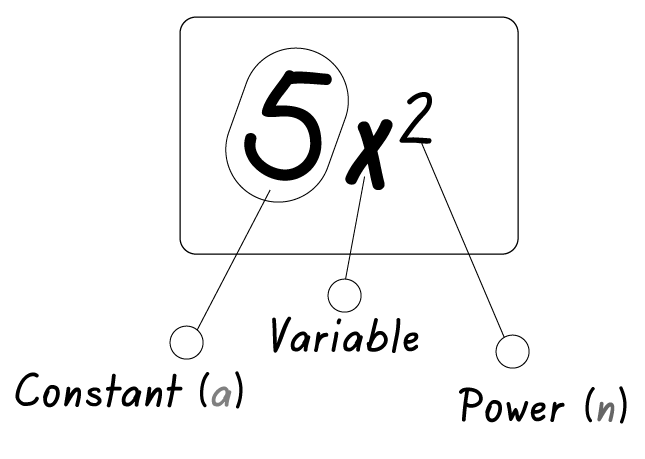
1. \frac{d}{dx}(5x^2 + 3x - 7) as 5x^2 + 3x - 7
2. \frac{d}{dx}(e^{2x} + \sin(x)) as e^(2x) + sin(x)
3. \frac{d}{dx}(4x \cdot \cos(x)) as x * cos(x)
4. \frac{d}{dx}\left(\frac{3x^2}{x+1}\right) as 3x^2/ (x+1)
5. \frac{d}{dx}(\ln(2x)) as ln(2x)
6. \frac{d}{dx}(10x \cdot \tan(x)) as 10x * tan(x)
7. \frac{d}{dx}\left(\frac{x^2}{\sin(x)}\right) as x^2/sin(x)
8. \frac{d}{dx}(e^{3x}\cos(x)) as e^(3x)\cos(x)
9. \frac{d}{dx}(x^3 \cdot \ln(x)) as x^3 * ln(x)
10. \frac{d}{dx}\left(\frac{2x+1}{x^2-3}\right) as (2x+1)/(x^2-3)
11. \frac{d}{dx}(5\sin(x) + 2\cos(x)) as 5*sin(x) + 2*cos(x)
12. \frac{d}{dx}(e^{4x} \cdot \tan(x)) as e^(4x) * tan(x)
13. \frac{d}{dx}\left(\frac{x^3}{\cos(x)}\right) as (x^3)/(cos(x))
14. \frac{d}{dx}(\ln(4x^2)) as ln(4x^2)
15. \frac{d}{dx}(7x^2 \cdot \sin(x)) as 7x^2 * sin(x)
16. \frac{d}{dx}\left(\frac{x}{e^x}\right) as x/e^(x)
17. \frac{d}{dx}(3\cos(x) - 8\sin(x)) as 3*cos(x) - 8*sin(x)
18. \frac{d}{dx}(e^{x^2}\cdot \csc(x)) as e^(x^2)*csc(x)
19. \frac{d}{dx}(x^4 \cdot \log(x)) as x^4 * log(x)
20. \frac{d}{dx}\left(\frac{3x-2}{x^3+1}\right) as (3x-2)/(x^3+1)
21. x = \sin(t), y = \cos(t) as x = sin(t), y = cos(t)
22. y^2 - \ln(x) = 0 as y^2 - In(x)
23. \frac{d}{dx}\left( \ln(2x) \right) as ln(2x)
24. \frac{d}{dx}\left( \sinh(x) \right) as sinh(x)
25. \frac{d}{dx}\left( \cosh(x) \right) as cosh(x)
26. \frac{d}{dx}\left( \tanh(x) \right) as tanh(x)
27. \frac{d}{dx}\left( \tanh(ax^2 + bx + c) \right) as tanh(ax^2 + bx + c)
28. \frac{d}{dx}\left( e^{\cos(x)} \right) as e^(cos(x))
29. \frac{d}{dx}\left( \log_a(x) \right) as log_a(x)
30. \frac{d}{dx}\left( \sin^{-1}(x) \right) as sin^(-1)(x)
- Differentiation from first principles
- Differentiation of y = ax n by the general
rule - Differentiation of sine and cosine functions
- Differentiation of eax and ln ax
- Methods of differentiation
- Differentiation of common functions
- Differentiation of a product
- Differentiation of a quotient
- Function of a function
- Successive differentiation
- Some applications of differentiation
- Rates of change
- Velocity and acceleration
- Turning points
- Practical problems involving maximum
and minimum values - Points of inflexion
- Tangents and normals
- Small changes
- Differentiation of parametric equations
- Some common parametric equations
- Differentiation in parameters
- Differentiation of implicit functions
- Implicit functions
- Differentiating implicit functions
- Differentiating implicit functions containing products and quotients
- Logarithmic differentiation
- Differentiation of logarithmic functions
- Differentiation of further logarithmic
functions - Differentiation of [ f (x)]
- Differentiation of hyperbolic functions
- Standard differential coefficients of
hyperbolic functions - Differentiation of inverse trigonometric
and hyperbolic functions - Inverse functions
- Differentiation of inverse trigonometric
functions - Logarithmic forms of inverse hyperbolic
functions - Differentiation of inverse hyperbolic
functions - Partial differentiation
- Introduction to partial derivatives
- First-order partial derivatives
- Second order partial derivatives
- Total differential, rates of change and small
changes - Total differential
- Rates of change
- Small changes
- Maxima, minima and saddle points for
functions of two variables