Differentiate x^(1/2) With Steps

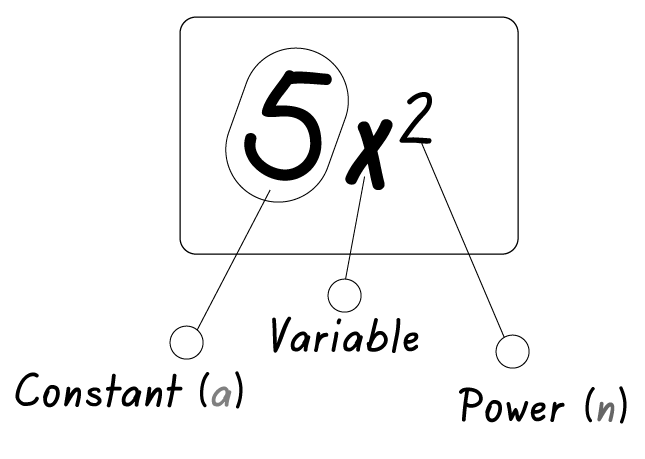
Differentiation of a √x

When we differentiate the function √x or x^(1/2), we use the power rule of differentiation.

Let y = √x or x^(1/2) , then we can rewrite y as y = x^(1/2).

To find the derivative of y with respect to x, we use the power rule which states that if y = x^n, then the derivative dy/dx = nx^(n-1).

Applying this rule, we have y' = 1/2  \cdot x^{- \frac{1}{2}}.

Therefore, the derivative of √x or x^{\frac{1}{2}}is 1/(2√x) or 1/(2x^\frac{1}{2}).

This means that the rate of change of the function √x is inversely proportional to 2 times the square root of x.

You can also differentiate coefficient of x in the following form

Common functions

7

6x

x^{1/2}

2x^2

Exponential functions

-e^{-\frac{12}{7x}}

-3e^{2x}

Trigonometric functions

4 \sin (x)

-\cos(3x)

Logarithmic functions

4In9x

1. Find the derivative of the function -2x^{-\frac{1}{2}}.

Solution:

To find the derivative of a function in the form f(x) = ax^n, where a and n are constants, we use the power rule. The derivative is given by:

f'(x) = n \cdot a \cdot x^{n-1}.

Applying this rule to the given function, we have:

f'(x) = -\frac{1}{2} \cdot -2 \cdot x^{-\frac{1}{2}-1}</p><p>= x^{-\frac{3}{2}}.

Therefore, the derivative of -2x^{-\frac{1}{2}} is

x^{-\frac{3}{2}}.

2. Determine the derivative of e^{x}.

Solution:

The derivative of e^{x} is itself, as the derivative of

e^{x} is e^{x}.

This is a unique property of the exponential function e^{x}.

Therefore, the derivative of e^{x} is

e^{x}.

3. Calculate the derivative of 4\cos(9x).

Solution:
By applying the chain rule and derivative of cosine function, we have:

f'(x) = -4 \cdot 9 \sin(9x) = -36 \sin(9x).

Therefore, the derivative of 4\cos(9x) is

-36 \sin(9x).

4. Find the derivative of -3e^{\frac{8}{5}x}.

Solution:

Similarly to the derivative of e^{x}, the derivative of e^{\frac{8}{5}x} is itself times the constant \frac{8}{5}:

f'(x) = -3 \cdot \frac{8}{5} e^{\frac{8}{5}x} = -\frac{24}{5} e^{\frac{8}{5}x}.

Therefore, the derivative of -3e^{\frac{8}{5}x} is

-\frac{24}{5} e^{\frac{8}{5}x}.

5. Differentiate the function 4\sin(2x).

Solution:

Using the chain rule and derivative of the sine function, we get:

f'(x) = 4 \cdot 2 \cos(2x)= 8 \cos(2x).

Therefore, the derivative of 4\sin(2x) is

8\cos(2x).

1. \frac{d}{dx}\left(-2x^{-\frac{1}{2}}\right) = x^{-\frac{3}{2}}

2. \frac{d}{dx}\left(-e^x\right) = -e^x

3. \frac{d}{dx}\left(4\cos(9x)\right) = -36\sin(9x)

4. \frac{d}{dx}\left(-3e^{\frac{8}{5}x}\right) = -\frac{24}{5}e^{\frac{8}{5}x}

5. \frac{d}{dx}\left(5\ln x\right) = \frac{5}{x}

6. \frac{d}{dx}\left(2x^3\right) = 6x^2

7. \frac{d}{dx}\left(9e^{-2x}\right) = -18e^{-2x}

8. \frac{d}{dx}\left(7\sin(2x)\right) = 14\cos(2x)

9. \frac{d}{dx}\left(-4e^{5x}\right) = -20e^{5x}

10. \frac{d}{dx}\left(3\ln(4x)\right) = \frac{3}{x}

11. \frac{d}{dx}\left(-5\cos(3x)\right) = 15\sin(3x)

12. \frac{d}{dx}\left(6e^{-4x}\right) = -24e^{-4x}

13. \frac{d}{dx}\left(2\sin(5x)\right) = 10\cos(5x)

14. \frac{d}{dx}\left(8e^{2x}\right) = 16e^{2x}

15. \frac{d}{dx}\left(4\ln(3x)\right) = \frac{4}{x}